General Information

Serial #

N/A

Part Number

1

Total Parts

2

AKA

N/A

Patents

N/A

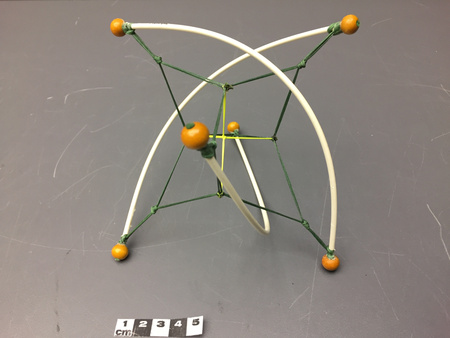
General Description

Spherical mathematical model given to renowned Canadian mathematician Donald Coxeter. Modèle mathématique sphérique donné au mathématicien canadien Donald Coxeter.

Dimensions

Note: These reflect the general size for storage and are not necessarily representative of the object's true dimensions.

Length

N/A

Width

N/A

Height

N/A

Thickness

N/A

Weight

N/A

Diameter

N/A

Volume

N/A

Lexicon

Group

Mathematics

Category

Models

Sub-Category

N/A

Manufacturer

AKA

ROBINSON

Country

Great Britain

State/Province

Unknown

City

Unknown

Context

Country

Canada

State/Province

Ontario

Period

This mathematical model was gifted to Donald Coxeter for his 90th birthday in 1997 and was used until his death in 2003.

Canada

This collection of models comes from the personal collection of H.S.M. Coxeter (1907-2003), one of Canada's more renowned mathematicians. At the age of sixteen, Coxeter won a prize for an essay on "dimensional analogy." This essay attracted the attention of Bertrand Russell, a friend of his father, and the young prodigy was promptly put on course for mathematics at Cambridge. He earned his B.A. there in 1929, and his Ph.D. in 1931 working under H.F. Baker. In 1936, Coxeter traveled across the Atlantic to join the Mathematics Department at Toronto, where he remained until his death in 2003. During his long career, Coxeter has made significant contributions to non-Euclidean geometry and to the theory of polytopes (the stretching of geometric shapes into higher dimensions). Many geometers today use what are called Coxeter groups, or groups that are generated by reflections.

Function

Used as a visual scientific representation of abstract mathematical ideas and theories. This model represents a challenging problem Coxeter posed to sculptor John Robinson in which five spheres in mutual contact where the points of contact form interesting mathematical relations in space.

Technical

John Robinson built Firmament derived from a challenging problem that Coxeter had posed to him related to five spheres in mutual contact where the points of contact form interesting mathematical relations in space. The models seem relatively simple in form, but for Coxeter even the most basic shapes represented difficult boundaries between higher mathematics and the world of everyday experience. This is a tension that Coxeter seemed to thrive on; he clearly saw things in the models that most others would find impossible to imagine, and this must be one of the main reasons that he has kept and displayed them. Coxeter certainly relied on the models as an aid for transmitting his ideas and as an entry into more abstract realms of mathematics. One can clearly see by the size and diversity of the collection, and by the fact that they were well-preserved and displayed, that Coxeter found them to be inspirational objects and springboards for an active mathematical imagination. They also represent a kind of three-dimensional correspondence with amateurs, students and artists reflecting the deep impact Coxeter had on twentieth-century geometry.

Area Notes

Unknown

Details

Markings

N/A

Missing

Appears complete.

Finish

Model made from four beige and light brown wooden spheres and one silver metal sphere. The top wooden sphere comes apart into two halves. The flat base of the model has a silver metal plate with a silver metal stem with three silver metal screws. Modèle fabriqué principalement de quatre sphères beiges et une sphère argentée en métal. La sphère de bois du dessus se sépare en deux moitiés. La base plate du modèle a une plaque argentée en métal avec une tige argentée en métal avec trois vis argentée en métal.

Decoration

N/A